Today's soundtrack is Figure Four: No Weapon Formed Against Us, a groovy hardcore album that was released in 1999. I'm still trying to wrap my head around the fact that 1999 was 20 years ago!
This afternoon, I'm going to be learning about Pascal's Triangle and the Binomial Theorem.
Pascal's Triangle is an interesting series of numbers that flows down like a pyramid. The first few rows look like this:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
...and so on...
Notice that the outer border is made up of all 1s. That continues on as far as we go down. But notice that each number inside of the borders is the sum of the two numbers above it. Each number indicates how many possible paths flowing down could have been taken to reach that point. We can add up all of the numbers on any given row to find the total number of pathways that could have been taken so far.
Pascal's Triangle has a fascinating relationship with the concept of combinations: each row follows the pattern of nCr. Looking at the sixth row in the triangle that I laid out above, our number series is 1, 5, 10, 10, 5, and 1. These numbers correspond with the results we would get from calculating 5C0, 5C1, 5C2, 5C3, 5C4, and 5C5. Notice that though we're on the sixth row which has six digits, my highest n was 5, and my highest r was also 5. This is an important concept to note: the relationship between the values of Pascal's Triangle and the combination formula require that we input n as one less than the desired row, and r as one less than the desired term.
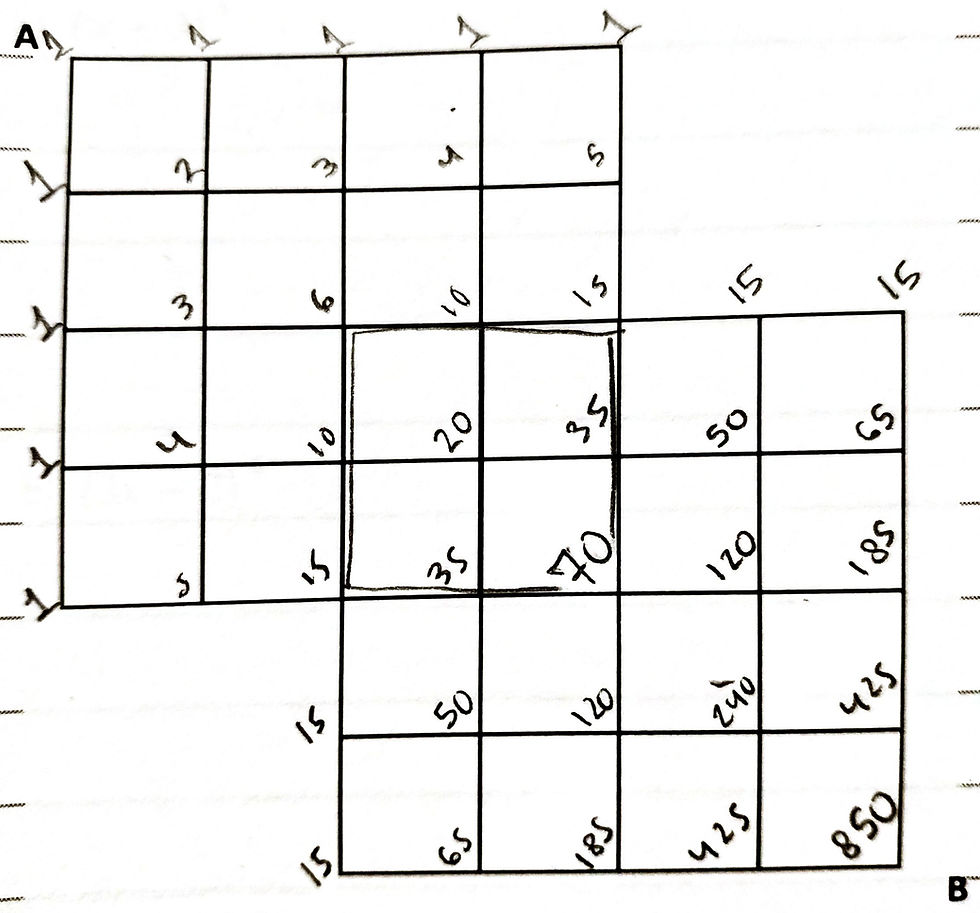
We can also use Pascal's Triangle to find the number of pathways from A to B in strangely-shaped objects, as long as we note that the border values don't change when they go in a straight line (see the 15s in the example on the right).
That's it for Pascal's Triangle; let's move on to binomial powers!
- - - - - - - - - -
Binomial powers are expressions in the form (a + b)ⁿ. n ≥ 0. They have a delicious property: When expanded, they are very clearly linked to Pascal's Triangle and the combination formula!
If we take (a+b)⁰, we get 1. (a+b)¹ is 1a + 1b. (a+b)² is (a+b)(a+b), which equals 1a² + 2ab + 1b², and so on.
There are several important things to point out about the expansion of binomial powers.
The first term (a) is the same in the equation as it is in the expansion
The exponent of the equation is the same exponent as we see in the expansion
The exponent of the first term (a) decreases by one each term
The second term (b) starts in the second position of the expansion
The exponent of the second term (b) increases by one each term
The coefficients in each row take the same form as the values of Pascal's Triangle
The numerical coefficients in the expanded form of (a + b)ⁿ can be found by using the equation nC0 + nC1 + nC2 + ... nCn.
Using this information, we can expand binomial powers much more quickly than we could through manual multiplication!
Isn't that great?!
I'm going to call it a night at this point; I've covered a lot of material here, and this chapter's a large one.
Next time, I'll continue the second part of this lesson.