Today's soundtrack is Gojira: L'Enfant Sauvage, a metal album that is heavier than four hundred million suns.
So I mentioned yesterday that I was having trouble figuring out what to do with trig identities with coefficients. I got some help from a friendly Redditor and was able to finally overcome the challenge. It turns out that the problem was never with the coefficients, but the fact that I entirely overlooked the fact that "1" needed to be rewritten into its Pythagorean form as shown below.
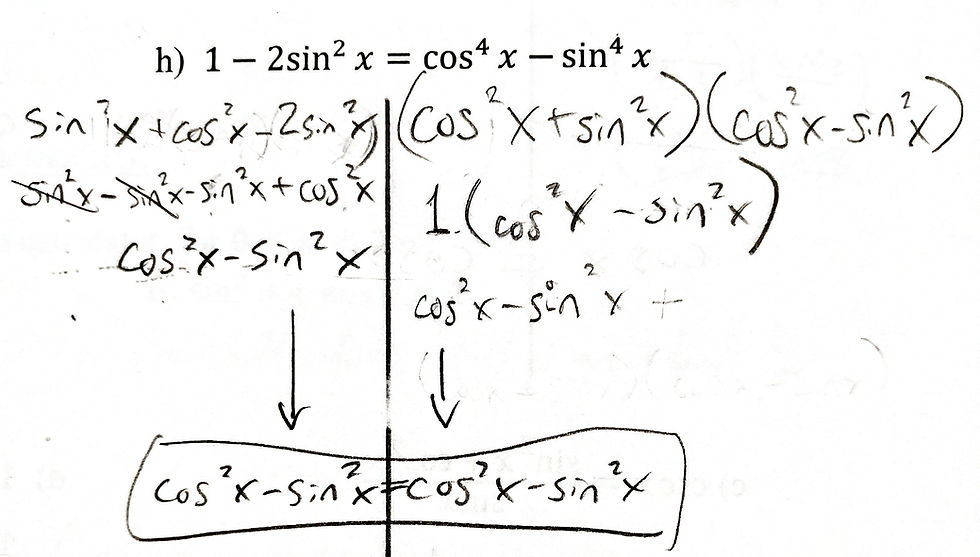
I'm now moving on to the next lesson: Sum and Difference Identities.
Expanding on the idea of trigonometric identities, we have sum identities and difference identities. These are sequences that equal each other. For example, sin (a + b) = (sin a cos b + cos a sin b). There are many of these identities.
To simplify an expression by adding and subtracting, we do the following:
Find the corresponding identity form
Substitute values into the identity form
Simplify, using exact values if possible
Sometimes we will need to expand and simplify. To do so, we follow these steps:
Find the corresponding identity form
Substitute values into the identity form
Find the values and simplify
We can use the sum and difference identities as we prove trigonometric identities. (I'm glad I took the extra time to really push through learning them before starting on this lesson!)
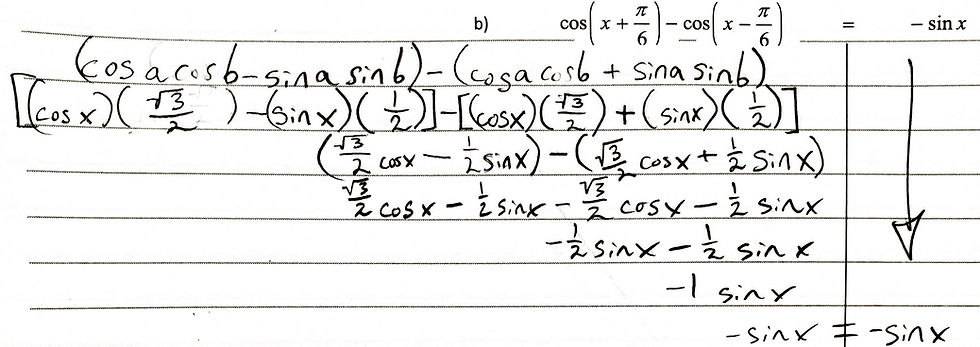
A final note: I had to do some extra research to figure this one out. (Thanks, Mathway!)
If we are asked to find the value of an inexact trigonometric ratio, such as cos(5π/12), we can start by splitting the value into two exact values, such as cos(3π/12 + 2π/12), which can be expressed as cos(π/4 + π/6). This makes it a sum identity, which we can proceed to solve by using the sum identity method.
That's it for today!
Next time, I'll be learning about double angle identities.