Today's soundtrack is Tegan and Sara: The Con, an album that reveals more of its true complexity and brilliance with every listen.
This afternoon, I'm learning about the different ways that we can change the graph of a trigonometric function.
There are some new terms that we'll be learning today. I want them all in one place, so here we go:
New Terms
Amplitude
Divergence from central axis
Vertical Displacement
Vertical translation
Phase Shift
Horizontal translation
Variable a
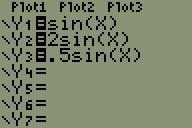
In yesterday's lesson, I mentioned amplitude, which is the maximum or minimum distance that the function diverges from its central axis. I learned today that there is an actual equation in place whereby we can calculate our function's amplitude: a = ([max-min] / 2).
So a represents a value that changes our function's amplitude. Let's try playing around with a as it modifies the function in the equation y=asin(x). If we multiply sin(x) by 2, we get a vertical expansion of 2. If we multiply sin(x) by 0.5, we get a vertical compression by a factor of 1/2. If we graph y=-sin(x), we will see a the original function reflected on the x-axis.
Modifications to a: Resulting Transformations
If a > 1, vertical expansion by a factor of a
If 0 < a < 1, vertical compression by a factor of a
If 0 > a > -1, reflect in x-axis and compress by a factor of a
If a = -1, reflect in x-axis
If a < 1, reflect in x-axis and expand by a factor of a
Variable d
Next, let's look at the effects that variable d has on our trigonometric functions. It will be either added or subtracted to our equation, and is placed at the end, like this: y=cos(x) + d.
d will once again transform our function vertically; this time, it will do so through vertical displacement of the function (moving the function up or down). We know that modifiers on the same side of the equation as the variable that they are connected to will be inversely related to their variables; since d modifies y but it is on the opposite side of the equation from y, d will simply translate the function up by d's value if d is positive, and will translate the function down by the value of d if d is negative.
To calculate the displacement of a graphed function, we substitute values and solve for d in the equation d = ([max+min] / 2).
Variable c
We're now moving on to horizontal transformations. The variable c transforms our trigonometric functions by being subtracted from x, like this: y=cos(x-c) + d. Because c is modifying a variable that is on the same side as itself, its values inversely affect x. So c in our equation results in a phase shift (horizontal translation) of the opposite of c's value. For example, if c was 2, we would phase shift left by two; if c was -3, we would phase shift right by 3.
If c > 0, phase shift left by c
If c < 0, phase shift right by c
That's it for today; next time, we'll continue learning more ways that variables can modify our trigonometric functions.