Today's soundtrack is Lil Wyte & Jelly Roll: No Filter, a collaborative rap album that I blasted in my car for months when I first got it. I was going through some rough stuff at the time, and this album helped me get through. I was working a stressful physical nightshift job at the time; when I was having one of them days; it helped me to stay strong and made me feel like I could move mountains, even when I was driving on the interstate, feeling all alone. I don't typically listen to a lot of rap, but I've been a fan of Lil Wyte since one of my buddies introduced me to his debut album, "Doubt Me Now," back in 2007. I hadn't heard Jelly Roll's material until this album, but he's got a really cool country rap style, which he acknowledges on one of the tracks, saying "I didn't know that I was country 'til I moved to California." The duo did an incredible job on this album; it's thoroughly enjoyable, and their styles really complement each other.
This afternoon, I'm learning about the sine, cosine, and tangent functions of special angles.
Most of the time, if we type in [function](angle), we'll get a decimal approximation rather than an exact value. Let's find out how to get an exact value of an angle's function. We'll start by evaluating a 30°-60°-90° triangle, which is so named because its three angles are 30, 60, and 90 degrees (or π/6, π/3, and π/2 radians). The ratios sides of a 30°-60°-90° triangle will always be 1, 2, and √3. If we used our calculator to find sin 60°, we would get 0.8660254038. But we can see by looking at the right triangle that since sin = opp/hyp, our exact value is √(3)/2.
Another triangle that we should be familiar with is the 45°-45°-90° triangle, which has sides 1, 1, and √2. In radians, this triangle is π/4-π/4-π/2. Its sin and cosine will be identical at 1/√2; its tangent will be 1.
Let's cut to the chase. 30° (π/6), 45° (π/4), and 60° (π/3) are all special angles; they are the only angles that can be written in exact terms. So if we start at 0°, every consecutive 30° gives us a special angle, as does every 45°. To put this concept into radians, if we start at 0, every π/6 gives us a special angle, as does every π/4. So let's draw a diagram that shows us every single special angle, all the way from 0°-360°. It's called the Trig Circle, and you can see my version of it below.
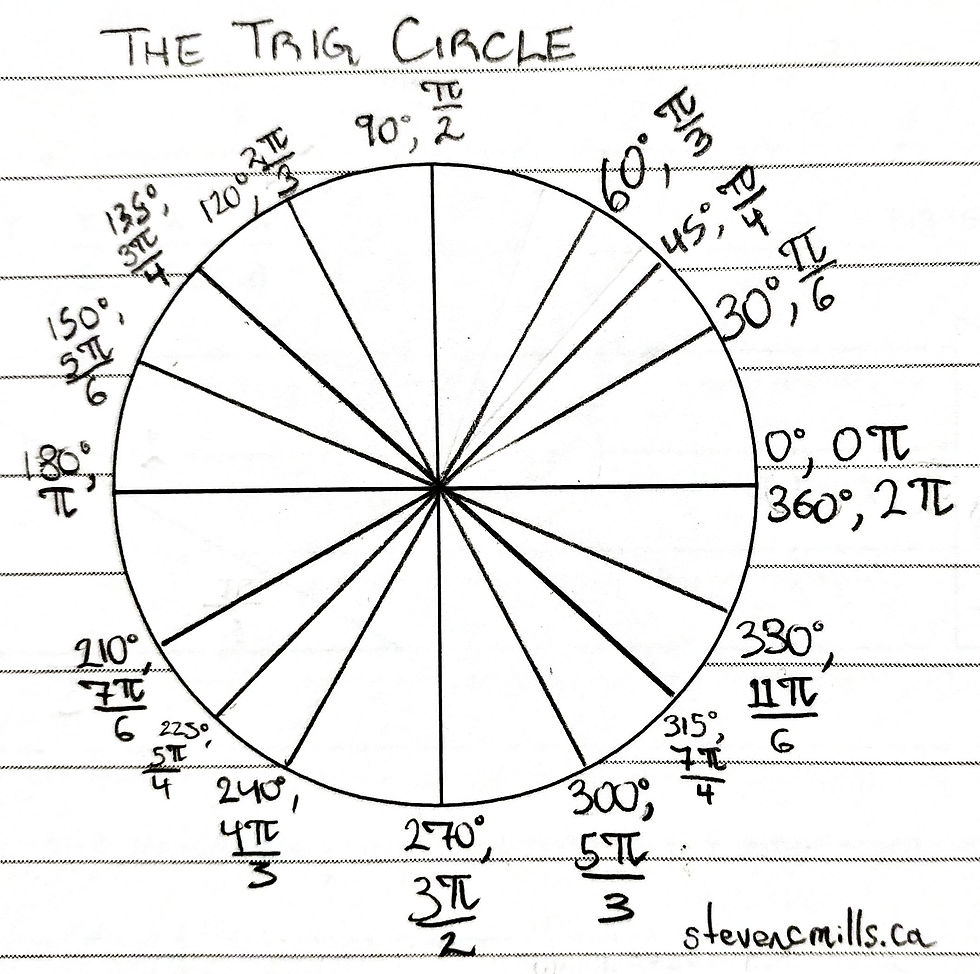
To make a trig circle, we start at 0°, then work our way around the circle counterclockwise, noting every multiple of 30°. We then do the same thing with every multiple of 45°. After we've noted down every special degree in angles, we can write out the conversions in radians. To do so, we simply start at 0, recognizing that every 30° is π/6, and 45° is π/4. Finally, we add up the radians at each noted point, then note their conversions next to the degrees.
So far, we've worked with the three trigonometry ratios: SINE (sin), COSINE (cos), and TANGENT (tan). Now we're going to learn about their reciprocal ratios.
Reciprocal Ratios
Cosecant
Written "csc"
Is the reciprocal of sine
csc θ = 1/(sinθ)
Secant
written "sec"
Is the reciprocal of cosine
sec θ = 1/(cos θ)
Cotangent
Written "cot"
Is the reciprocal of tangent
cot θ = 1/(tan θ)
Rather than manually working out which portions of an angle are positive and negative, we can use a simple mnemonic to quickly determine which ratios are positive or negative in the four quadrants. The phrase we need to remember is "All Students Take Calculus." The first letter of each word (ASTC) corresponds with a set of ratios and with a quadrant. What we need to know is this: the positive ratios in quadrants 1, 2, 3, and 4 are All, Sine, Tangent, Cosine. Another way to remember this is that if we start in quadrant 3 and work our way counterclockwise, we can use the word "CAST" to remember the same thing. You can use whichever method is easier to remember!
When we encounter an assignment, test, or quiz where we know that we will be asked to determine exact values of trigonometric functions, we need write out four pieces of information before we begin:
The Trig Circle with both degrees and radians
The 30°-60°-90° triangle with both angles and sides
The 45°-45°-90° triangle with both angles and sides
The 3x3 sin/cos/tan, 30°/45°/60° chart
Once we have all of those pieces of information listed, we can use them to solve various questions related to exact values of various ratios. For example, if we are asked to find the exact value of sin(5π/4), we will do the following:
How to Determine the Exact Value of a Specific Trigonometric Ratio
Locate the ratio on the trig circle
Looking at my trig circle, I can see that sin(5π/4) = 225°
Find the reference angle
The shortest angle between 225° and the x-axis (180°) is 45°
Use the ratio/angle chart to find the corresponding value
According to the chart, sin(45)'s exact value is 1/√2
Use either CAST or ASTC to determine whether the ratio is positive or negative in the original quadrant
225° is in Quadrant III; according to ASTC, the only positive ratio in the third quadrant is Tangent, so Sine is negative; this gives me my final answer: -1/√2
IMPORTANT NOTES:
- If given a positive radian that isn't on the trig circle, try subtracting 2π.
- If given a negative radian that isn't on the trig circle, try adding 2π.
- If given an angle that is on an axis, no reference angle needs to be found.
That's it for today; tomorrow, I'll be learning how to graph the sine and cosine functions.