Today's soundtrack is Brahms: Symphony #4.
This afternoon, I'm learning about angles in standard position. Some of the terminology will be familiar, as I covered angles in standard position in these three lessons back in January.
We can measure the angle of something either in degrees or in radians. What is a radian, though? To answer that, we must first invent the universe. No, wait. We're talking about radians, not apple pie. Though we will be talking about pie later. Well...actually, no. But we'll talk about pi, and that's even more fun (though less tasty, unless we're talking about pi of pie).
But for now, before we can define a radian, we need to first be able to identify a radius. The radius is the distance from the centre of a circle to its outer edge - think of the spoke of a bicycle wheel. Now imagine that you wanted to measure the distance of one of the bicycle spokes, but you don't have a tape measure; all you have is a yardstick, and the yardstick is superglued to a table, so there's no feasible way to measure the spoke of the wheel. What do you do? You grab some string, pull the string taut from the wheel's hub to the tire, snip it at the wheel, then take it inside and measure it against your yardstick. That's your wheel's radius. Now suppose you want to find the radian. You would walk back outside, stretch that same length of string as far as it'll go outside of the rim of the wheel, and mark off both sides. That's the length of your radian. So the radian is the same length of the radius, but curved.
Check out the awesome, high-tech graphic below for a visualization.
Now suppose you flipped that string end-over-end like a slinky to measure the circumference (outer border) of the wheel. It would take just over six lengths of that string to make it all the way around. It follows, then, that it would take just over three lengths of the string to go halfway around the wheel (180°). To be more precise, it would take approximately 3.14 lengths of string. Does that number look familiar? It's the first three digits of pi (π).
Let's take a moment to sum up what we've covered so far. It takes 3.14 times r (our radius' length) to equal half of our circle's circumference; therefore, it takes 2(3.14)r to go all the way around. So let's phrase this more mathematically: πr = 180°, and 2πr = 360°. Taking this one step further, letting C = our circumference, C = 2πr.
Let's compare the four major angles with their corresponding measures in radians.
0°, or 360°
0, or 2π
90°
π/2
1/4 of 2π
180°
π
1/2 of 2π
270°
3π/2
3/4 of 2π
Converting Radians to Degrees: radians(180°/π)=d
We know that 180° = π radians. We can divide both sides by π, then restate this as 1 radian = 180/π. To convert radians to degrees, we let d = degrees, then we calculate radians(180°/π)=d.
For example, if I have 4 radians, I multiply 4 by 180°, which is 720°. 720°/π is 229.18°. Therefore, 4 radians = 229.18°.
Converting Degrees to Radians: 1°=π/180 radians
On the flip side of that, we can convert degrees to radians. Remembering that 180° = π radians, we can divide both sides by 180 and restate this as 1°=π/180 radians.
If I wanted to know how many radians 135° was equal to, I would multiply both sides of my equation by 135, giving me 135(1°)=π/180(135). This works out to 135°=135π/180. Both 135 and 180 are divisible by 45; thus, our answer is 135°=3π/4 radians, which can be stated as 2.36 radians.
Determining Arc Length: a=rθ
We're now going to investigate a circle's arc length. An arc's length divided by a circle's circumference is equal to the ratio of the angle divided by 2π. If we have a circle with an angle indicated, where the arc length is a, the angle is θ, and the radius is r. We can represent this with the equation a=rθ.
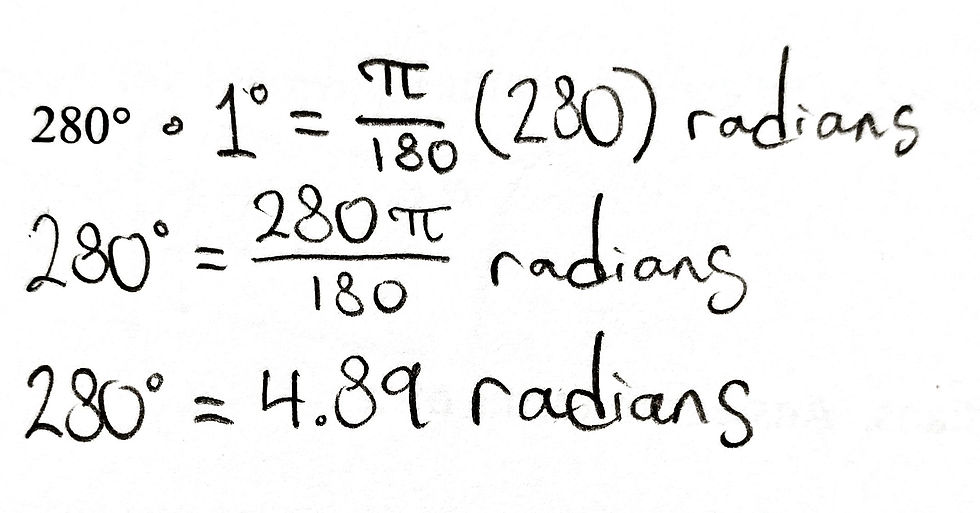
If I want to find the length of an "arc that subtends an angle of 5.2 radians at the center of a circle with radius 12.7 cm" (Pre-Calculus 12, Unit 5, Lesson 1, Page 4), I would begin by substituting the known information into the equation a=rθ. My arc is a, which I'm solving for. θ is the angle, which in this case will be 5.2 radians. My radius, r, is 12.7cm. So we'll solve for a in the equation a = (5.2)(12.7). 5.2 times 12.7 is 66.04; thus, our arc length is 66.04cm.
An important note: If theta is given in degrees instead of radians, we must first convert the degrees to radians before proceeding.
Angles in Standard Position
To draw an angle in standard position, our initial arm is on the positive x-axis. Our terminal arm (the one that swings about) goes counterclockwise if θ > 0, and clockwise if θ < 0.
While we work with angles in standard position, we will come across coterminal angles, which just means angles that end up in the same place together. We're already familiar with this relationship: 0° and 360° are on the same place. This is a coterminal angle. 20° and 380°, 380° and 750°, -10° and -370° - each of these is an example of a coterminal angle. There are infinite possibilities. The properties of coterminal angles are as follows:
They have the same initial arm
Their terminal arms end in the same place
There is 360° between them
We can represent the relationship between coterminal angles with the equation θ + n(360°), n∈Z (integers) if theta is in degrees, or θ + n(2π), n∈Z, if theta is in radians.
That's it for today! Next time, we'll be looking at functions of angles in standard position.