03.19.2019: One Lesson of Math - Polynomials, 3/5: Factoring Polynomials
- Steven C. Mills

- Mar 19, 2019
- 7 min read

Today's soundtrack is Our Lady Peace: Happiness...Is Not a Fish That You Can Catch, an album that I like well enough, but it's never really clicked with me for reasons that I can't quite put my finger on.
Today's been great so far; we took the kids out to a local show in the morning, and now it's time to buckle down to work. This afternoon, I'll be reviewing factoring polynomials - more specifically, how to recognize which method to use in which case.
There are some basic polynomials that we all already know from earlier courses: simple quadratic trinomials (x² + 3x - 4), "messy" quadratic trinomials (those where the coefficient of x² ≠ 1), and Difference of Squares polynomials (x² - 9).
Just as a refresher, let's go through the steps to factor each one.
How to factor a simple quadratic trinomial
Create two sets of brackets with x at the left side of each one
(x ) (x )
Find two numbers whose product equals the constant and whose sum equals the middle term
If given the trinomial x² + 3x - 4, we can see that, since our constant is negative, one of our factors will be negative. So our options for two numbers that come to negative four are 1 and -4, 2 and -2, or 4 and -1. Our factors need to have a sum of 3, our centre term. 1 and -4 has a sum of -3, ruling out those possible factors. 2 and -2 comes to 0. But 4 and -1 gives us 3!
Input the two factors, including their positive or negative symbols, into the two brackets
Since our two factors are -1 and 3, our factors are (x-1) (x+3).

How to factor a messy quadratic trinomial through decomposition of factors \M/
Create two sets of brackets with x at the left side of each one
(x ) (x )
Multiply the coefficient of the x² term by the constant
Given the trinomial 6x² - 13x + 5, we multiply 6 by 5, giving us 30
Find two numbers whose product equals the product of the coefficient and the constant found above, and whose sum equals the coefficient of the middle term
Since 30 is positive and 13 is negative, we know that both factors must be negative; thus, we need to find two negative numbers which equal 30 when multiplied and equal 13 when added together. -15 and -2 multiply to equal 30, but added together, they equal -17. Close, but no banana. What about -10 and -3? Their product is 30; their sum is -13. Bingo!
Rewrite the equation, including the newly found terms as coefficients of our centre variable
Since these -3 and -10 are actually a rewritten form of our middle term (-13x), we rewrite our equation 6x² - 13x + 5 as 6x² - 3x -10x + 5
Factor the first two terms and the second two terms, ensuring both sides have the same value inside brackets
6x² - 3x gets factored as 3x(2x-1); -10x + 5 gets factored as -5(2x-1). Both sets of brackets are identical; we are ready to proceed.
Put the terms outside brackets into a new set of brackets, multiplied by the identical brackets
3x and -5 are outside of brackets, so we put them into new brackets: (3x-5)
We multiply the new bracketed items by the existing bracketed items: (2x-1)
Our final answer is (3x-5)(2x-1).
How to factor a Difference of Squares
Create two sets of brackets
( ) ( )
Find the square root of each given coefficient
Given the polynomial 64x² - 81y², we get (8x)² - (9y)²
Inside the empty brackets, add the two terms together in the first bracket, and subtract one term from the other in the second bracket
(8x - 9y) (8x + 9y)
Now that we've reviewed factoring polynomials, let's move forward.
The first rule of factoring is to remove a common factor if possible! Because we aren't often given polynomials with common factors, it's easy to forget this step, but looking for common factors in messy polynomials will, in the few cases that we find one, save us a lot of time and effort. One important thing to keep in mind is that the removed factor is still a factor, and it must be kept in the list of factors. For example, in the trinomial 5x² - 10x - 15, we can see that 5 can be factored out, giving us 5(x² - 2x - 3), a simple trinomial, which can be factored as 5(x+1)(x-3).

The second rule of factoring is to factor your factors after you factor. What do I mean by this? Well, take for example x⁴ + 3x² - 28. We can factor it into (x² + 7) (x² - 4). But look more closely at that second bracket! x² - 4 is a classic Difference of Squares! We can factor this factor into (x + 2) (x - 2), so our factored final form is (x² + 7) (x + 2) (x - 2).
For me, this next one was a new concept: the Difference of Cubes, which is closely related to the Difference of Squares (see the section next to Mr. Whittaker, above). The Difference of Cubes takes the form a³ - b³, and its factored form is (a - b) (a² + ab + b²). Some examples of Difference of Cubes are: 64x³ - 125y³, 1 - 216g³, and x³ - 8. Even 54 - 128b³ can, considering our second rule of factoring, be found to be a kind of difference of cubes, since 54=2(27), and 128 is 2(64), and 27 is 3³, and 64 is 4³. Let's go through the steps of factoring a Difference of Cubes.
How to Factor a Difference of Cubes
Find the cubed value of each coefficient
Given 64a³ - 125b³, we know that our two cubed values are 4a and 5b.
Put the cubed values into the factored form
The factored form is (a - b)(a² + ab + b²)
Inserting 4a and 5b, we get (4a - 5b)([4a]² + [4a][5b] + [5b]²)
Simplify
Our final factored form is (4a - 5b)(16a² + 20ab + 25b²)
The next step after learning to recognize and factor a Difference of Cubes is learning to recognize and factor a Sum of Cubes. The Sum of Cubes takes the form a³ + b³, and its factored form is (a + b)(a² - ab + b²). A Sum of Cubes looks identical to a Difference of Cubes, except that instead of one being subtracted from the other, the two terms are added together. Examples of Sums of Cubes are 64x³ + 125y³, 1 + 216g³, and x³ + 8. Even 54 + 128b³ can, considering our second rule of factoring, be found to be a kind of Sum of Cubes, since 54=2(27), and 128 is 2(64), and 27 is 3³, and 64 is 4³.
Just to make things clear as mud, let me sum it up here:
Difference of Cubes
(a³ - b³) = (a - b)(a² + ab + b²)
Sum of Cubes
(a³ + b³) = (a + b)(a² - ab + b²)
Up next is factor by grouping. If we have four terms in a polynomial, we can group like terms and factor by grouping. For example, if given x³ + x² - 2x - 2, we can see that x² is a factor of the first two terms, and 2 is a factor of the second two terms. So if we note x² as a factor of the first two terms, we get x²(x+1); if we write -2 as a term of the second two terms, we get -2(x+1). In the same way that we do with Decomposition of Factors, we put the two terms that aren't in brackets into new brackets together, and group the other two identical brackets, giving us our final answer: (x + 1)(x² - 2).
But what if we have a four-term polynomial that doesn't produce a common binomial? Take x³ - 3x² - 6x + 8. It produces the factors x²(x-3) and -2(3x+4). We can't factor it by grouping, obviously. But we can use our new-found skill: employing the Factor Theorem to find a root! And if we can find a root, we can find a factor. So like we learned yesterday, we find all of the potential roots of our constant, 8. Then, using synthetic division, we see which ones produce no remainder. Let's walk through the steps:
How to use synthetic division to find the factors of a polynomial
List all possible factors, considering the Factor Theorem and the Rational Zero Theorem
Given the equation x³ - 3x² - 6x + 8, all possible roots are based on the constant 8, and they are ±1, ±2, ±4, and ±8
Use Synthetic Division to divide the equation by the various possible roots; convert a root which does not produce a remainder into factored form
1 produced no remainder; thus, it is a root; therefore, (x-1) is a factor of the equation.
Rewrite the equation, using the bottom-row terms from the synthetic division chart as the coefficients of the variables (and the last term, not including the 0 remainder, as the constant), preceding the equation with the root found in Step 2
In my synthetic division table of the above equation, I ended up with 1, -2, -8, and 0 in my bottom row. 0, of course, is the remainder; we ignore it.
I rewrite the equation as (x-1)(x²-2x-8).
Fully factor
We can see that x²-2x-8 is a simple trinomial; we can factor it to (x-4)(x+2); remembering to add our factor found in Step 2, our final answer is (x-1)(x-4)(x+2).
Sometimes we'll come across a strange polynomial that looks like it should be factorable, but it just isn't - for example, x³-7x-6. It looks like a simple trinomial, but there are no two factors whose product equals -6 and whose sum is -7. In cases like those, we can do the same as above: use the factor theorem and synthetic division! Factors with five terms or more must also be solved via synthetic division, and we might even need to repeat the steps more than once (see the example below).
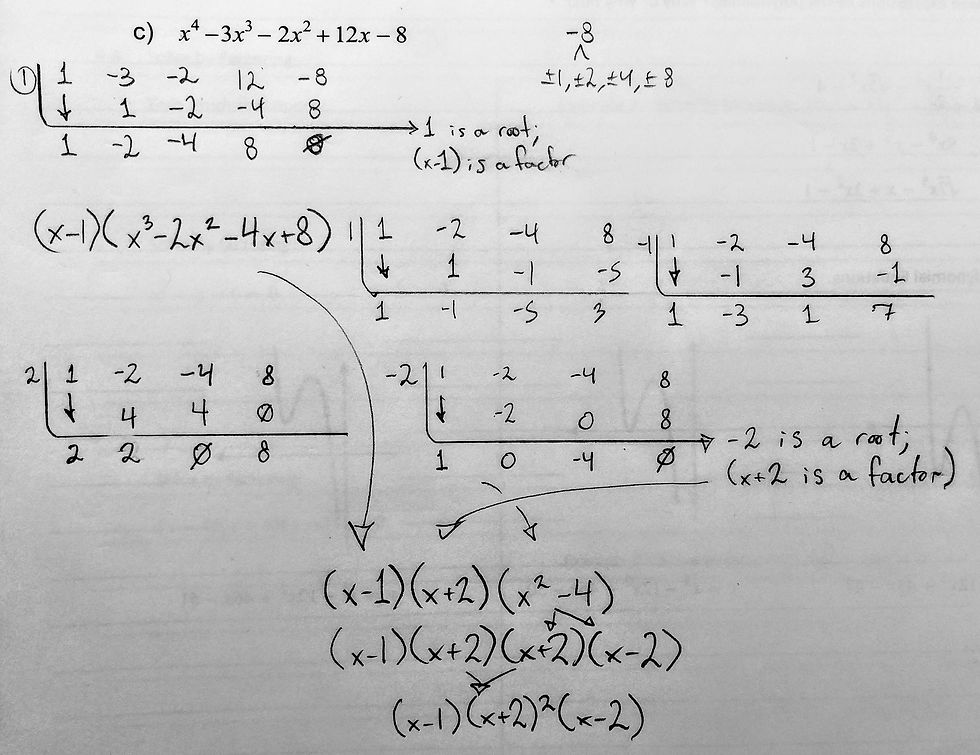



Comments