03.10.2019: One Lesson of Math - Radical and Rational Functions, 5/6: Analysing Rational Functions
- Steven C. Mills

- Mar 10, 2019
- 1 min read

Today's soundtrack is Andrew W.K.: The Wolf, an epic party rock album that is both self-assured in its grandiosity and awash in fun.
This morning, I'm learning how to analyse rational functions.
If a factored function has common factors in the numerator and denominator, we will get a point of discontinuity. If the factored function does not have any common factors, we will have a vertical asymptote.
I learned that not only can we draw a graph based on an equation, we can also write up an accurate equation based on a graph, going so far as being able to identify points of disconnects, x- and y-asymptotes, etc.
Here's how it works: we know that the rational equation is in the form y = (a / [x - h]) + k. So we just need to know what items go where. If we see a disconnect on the graph, we identify its x-value, invert it, and pop it inside some brackets on both the numerator and denominator. If there's an x-intercept, it goes inside brackets in the numerator. If we have a vertical asymptote, it goes in the denominator inside another set of brackets.
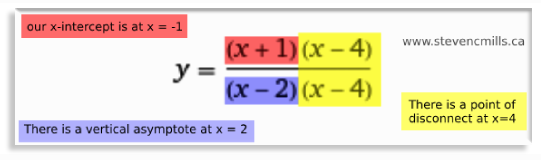



Comments