Today's soundtrack is Parquet Courts: Wide Awake, a fun and funky punk-inspired indie rock album.
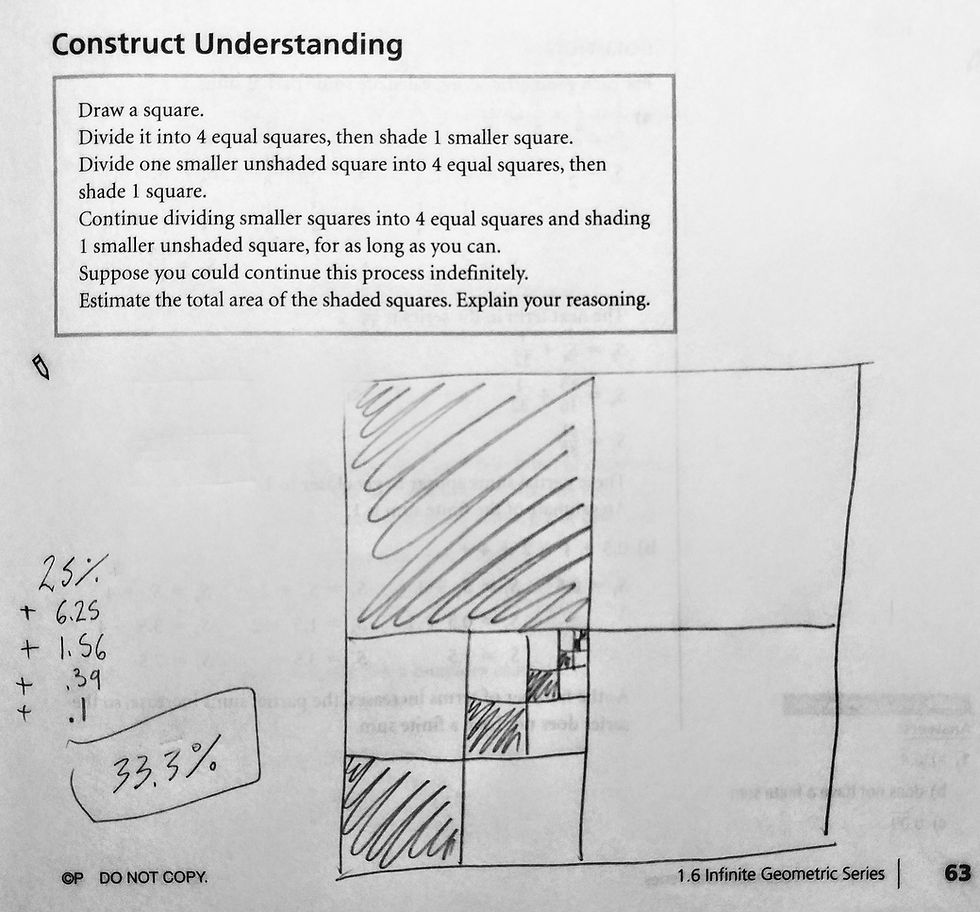
This afternoon, I'm learning about infinite geometric series. We learned in this September post that geometric sequences can be either finite or infinite; by extension, we would assume that the associated geometric series would also be either finite or infinite, depending on which the sequence was. Interestingly, this is not always the case.
A finite geometric sequence will always have a finite geometric series, but the sum of an infinite geometric sequence's geometric series will actually be classified as finite in some cases!
The way that this works is that though we know that the numbers go on forever, in some cases, the sum in each higher term "converges to a constant value" (Pearson, "Pre-Calculus 11," p. 64). We estimate the final sum based on the number that the term sums seem to be moving toward. Because geometric series work exponentially, we know that, for example, a series that moves toward 0 will never actually reach zero. It just moves toward zero. No matter how far we go, it will never actually reach 0; we'll just see more and more 0s before our number: eg, 0.000000000000000000001.
When the sum of an infinite geometric series converges on a constant value, we call the estimated sum "the sum to infinity" (p. 64); it is shown as S∞.
To determine whether a geometric series has a finite sum, we calculate some partial sums. If they seem to be converging, we estimate the finite value that the series is converging upon.
I had a really hard time estimating the finite sums of converging infinite series, so I'm trying something out. I'm going to find the tenth sum of each converging geometric series, because that should be far enough in the future to find the right answer. I'm using the general formula for a series: Sn = t1(1-[r]ⁿ)/1-r, r≠1 and solving for S10. It works.
The general formula for an infinite geometric series is S∞ = t1 / 1-r.
